Dreieck

Ingenieurgeograph

Freitag, 10. Oktober 2014

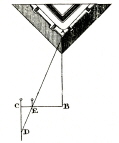
Aufgabe

Die Entfernung mit dem Stab über ein Dreieck zu nehmen.

Lösung

In der nachfolgenden Aufgabe ist Entfernung einer Batterie zur ausspringenden Spitze (Saillant) einer Bastion zu finden:

Neunzehnte Aufgabe: Man soll die Distanz AB des verlängerten Kapitals des Bollwerks von der Spitze der Gräben zum Winkel A messen.

Man ziehe BE senkrecht auf AB, und lege von B bis E 100 Fuß, verlängere BE bis C, und mache EC gleich dem achten oder zehnten Teil von BE; bei C richte man die senkrechten Linie CD auf. Stelle Stäbe bei E und C, dann gehe man mit einem anderen Stabe auf CD, bis dieser Stab in einer Linie mit E und A ist. Man messe CD, und man wird die Länge von AB durch folgendes Verhältnis erhalten, wie EC:CD = BE : AB; z.B. wenn BE = 100 Fuß, EC 10 Fuß und CD = 38 Fuß, so ist 10:100 = 38:380 Fuß, als Entfernung von AB.

Isaac Landmanns Abhandlung über praktische Geometrie beim Militair, in: George Adams, Geometrische und graphische Versuche oder Beschreibung der mathematischen Instrumente, deren man sich in der Geometrie, der Zivil- und Militär-Vermessung, beim Nivellieren und in der Perspektive bedient., Leipzig 1795, S. 259

Meine Anmerkungen hierzu:

Das Grundprinzip ist die Konstruktion sog. Ähnlicher Dreiecke im Gelände. Ähnliche Dreiecke sind solche mit drei gleichen Winkeln, wo dann die Seiten des verkleinerten und ausgemessenen Dreiecks sich zueinander wie die Seiten des größeren Dreiecks verhalten. In der unteren Abbildung: das große Dreieck EBA und das kleinere Dreieck CED, deren Seiten sich wie 1:10 verhalten.
Die eiserne Meßkette können auch durch ein Hanf- oder Strohseil ersetzt werden. Entfernungen wurden üblicherweise durch Abschreiten bestimmt, weswegen die Distanzen in der Regel in Schritt bestimmt wurden.
Die Linie BEC wird wie in der Landmesserei üblich durch Fluchten bestimmt.
Für die Stäbe genügen in etwa mannshohe Stecken.
Die 2 geforderten rechten Winkel konnten durch einen Winkelspiegel, durch „Abklatschen“ oder durch ein Seil nach Pythagoras bestimmt werden, was das einfachste ist: Man unterteilt das Seil in willkürlichen Einheiten im Verhältnis 3:4:5, bestimmt die Endpunkte durch Knoten, durch welche man die Stäbe stecken kann, so wird man leicht ein rechtwinklichtes Dreieck konstruieren können. Das Abklatschen kommt aus dem Bauwesen: Man stellt sich auf die Linie, schlägt beide Arme zusammen und bestimmt den Gehilfen in besagter Direktion den Stab in die Erde zu stecken.
Diese Messung ist an allen Orte mit den einfachsten Hilfsmitteln in etwa 5-10 Minuten durchführbar, vorausgesetzt, man die ebene Fläche für das Hilfsdreieck und kann von allen Stationen die Zielpunkte anvisieren.
Das Verfahren kann leicht erweitert werden, um zum Beispiel die Ausdehnung einer Stadt, die Breite eines Flusses oder die Distance einer entfernen Batterie zu bestimmen.
Das Verfahren erfordert nur Division und Multiplikation, ist also das einfachst mögliche, und zudem erheblich genauer als das Abschätzen mit der Mikrometer-Skala.
Das Verfahren wurde sicherlich nur an festen Positionen angewendet, beispielsweise um die Entfernung der Zielpunkte in Reichweite der Geschütze zu bestimmen, also insbesondere bei Belagerungen.

Ergebnis

Die Entfernung von der Bollwerksspitze zur Batterie wird mit 380 Schritt bestimmt.

Distanzmessung

Spitze der Molenbastion